Oxbridge-Science-Academy.github.io

Differential Equations

Back to Chemical Kinetics Home
Copyright Oxbridge Science Academy 2022

A key progression from high school to university is thinking about rates with a more quantitative mindset. This is done by linking the two different rate equations – the differential equation and the power law equation.

Consider the simple reaction $\displaystyle X \rightarrow Y$

We can express the rate of reaction as:

$\displaystyle rate=k[X]$

$\displaystyle rate=-\frac{d[X]}{dt}$

Equating these expression, we can write:

$\displaystyle \frac{d[X]}{dt} = -k[X]$

Solving this differential equations allows us to describe how the concentration of a particular reactant, in this case X, varies over time. This approach can also be used for intermediates and final products and is important in many fields. In pharmacology it is necessary to know how quickly a drug is destroyed in the body to calculate the required dosage while the field of atmospheric chemistry is centred around the production and destruction of chemical species in the atmosphere. We can also use knowledge of how a concentration should vary over time to calculate, from experimental data, the order of a reaction with respect to a particular species.

1st Order Reactions

Consider the reaction $\displaystyle X \rightarrow Y$ which is 1st order with respect to $\displaystyle X$

As discussed above we can write:

$\displaystyle \frac{d[X]}{dt} = -k[X]$

Consider the resulting differential equation - we can solve this using the method of separation of variables. (See Integration course if you have not encountered this method before)

$\displaystyle \int \frac{1}{[X]} d[X] = -k \int dt$

The integral can be treated as indefinite for now, resulting in:

$\displaystyle \ln [X] = -kt +\ c$

Where we have combined the two constants of integration into on constant, $\displaystyle c$ .

To assign a value to this constant, we consider the boundary conditions. At the start of the reaction $\displaystyle t=0$ and the concentration of $\displaystyle [X]$ was some initial value $\displaystyle [X]_0$ .

Substituting these values into the equation directly above, we arrive at:

$\displaystyle \ln [X] = -kt +\ \ln [X]_0$

Removing the natural logarithm by raising $\displaystyle e$ to the power of each side results in:

$\displaystyle [X] = [X]_0 e^{-kt}$

Thus we arrive at the conclusion that a species which is destroyed in a first order reaction will have its concentration decay exponentially with time. This is precisely the same as the mathematics behind radioactive decay of unstable nuclei since the act of decay is a first order process.

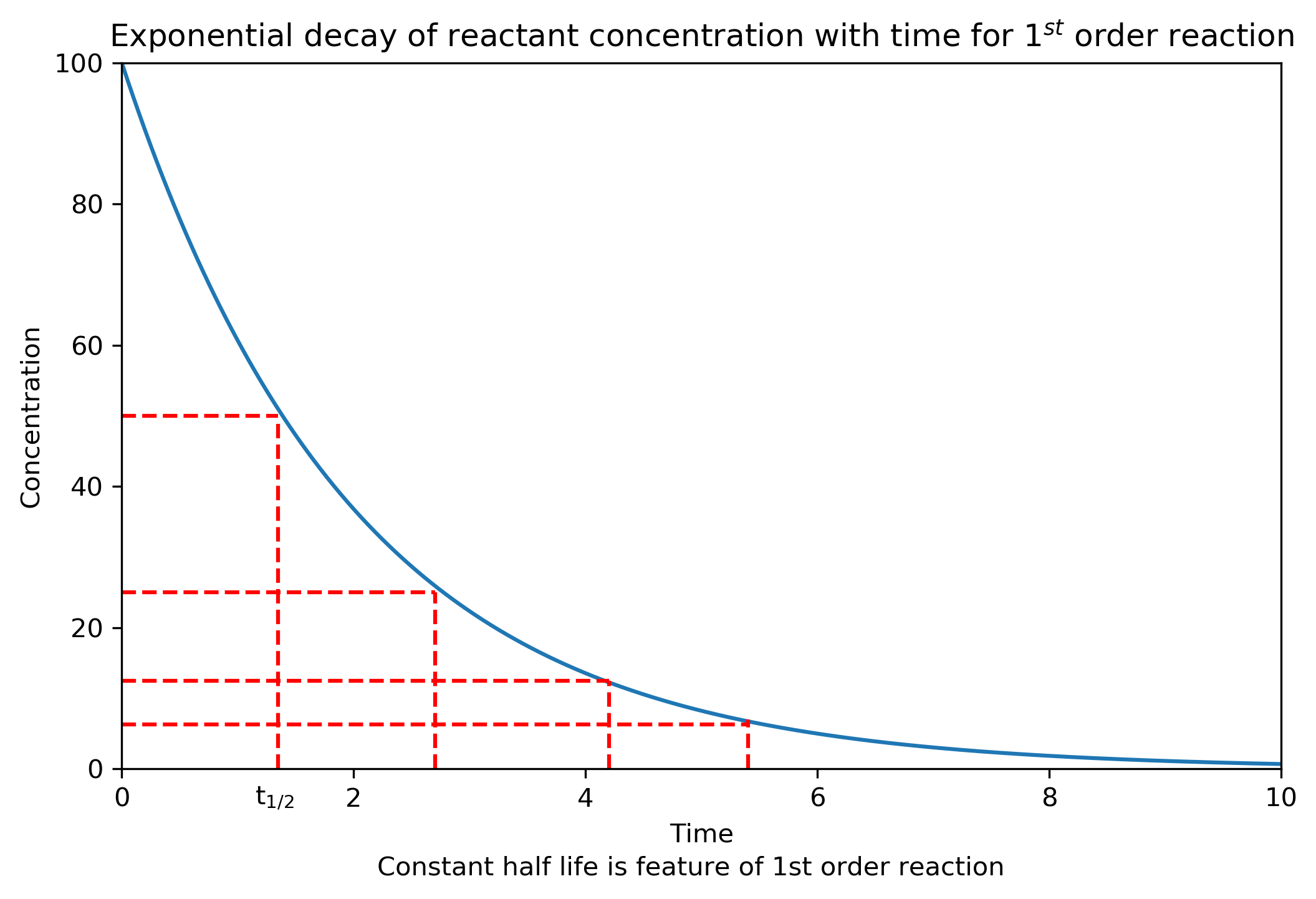
Exponential decay has several important implications including the fact that concentration of reactant is predicted never to quite reach zero and secondly the half life of the species is constant (not the case for other orders of reaction).

The plot below shows the concentration profile for a first order reactant with a half life of ~1.5 s. The dashed red lines show visually that the half life is constant.

alt text

2nd Order Reactions

Consider the reaction $\displaystyle X +\ X \rightarrow Y$ which is 2nd order with respect to X and has second order rate constant $\displaystyle k_{2nd}$ . We can relate the power law and differential forms:

$\displaystyle rate = -\frac{d[X]}{dt} = k_{2nd}[X]^2$

Consider the differential equation - again, we can solve this using the method of separation of variables. (See Integration course if you have not encountered this method before)

$\displaystyle \frac{1}{[X]^2}d[X] = -2 k_{2nd}dt$

Integrating both sides indefinitely:

$\displaystyle \int \frac{1}{[X]^2}d[X] = -2 k_{2nd} \int dt$

$\displaystyle -\frac{1}{[X]} = -2 k_{2nd}t +\ c$

Again, to assign a value to the constant of integration, we consider the boundary conditions. At the start of the reaction $\displaystyle t=0$ and $\displaystyle [X] = [X]_0$ . Substituting these values into the equation directly above, we arrive at:

$\displaystyle -\frac{1}{[X]} = -2 k_{2nd}t - \frac{1}{[X]_0}$

This can be rearranged to give:

$\displaystyle [X] = \frac{[X]_0}{kt[X]_0 +\ 1}$

It is helpful to consider whether this final expression makes sense. At the start when $\displaystyle t=0$ , the expression predicts $\displaystyle [X] = [X]_0$ as required and as $\displaystyle t \rightarrow \infinity$ , the denominator also $\displaystyle \rightarrow \infinity$ and $\displaystyle [X]_0 \rightarrow 0$ as required.

Zero Order Reactions

Consider a reaction $\displaystyle X +\ Y \rightarrow Z$ . While this may look first order in both $\displaystyle X$ and $\displaystyle Y$ , in this particular let’s say that there are two steps involved. The first involves $\displaystyle X$ decaying into another product, $\displaystyle X^*$ before $\displaystyle X^*$ reacts with $\displaystyle Y$ :

$\displaystyle 1. \\ X \rightarrow X^*$

$\displaystyle 2. \\ X^* +\ Y \rightarrow Z$

In this case, the first step is the RDS so the reaction is zero order with respect to $\displaystyle Y$ ; in other words the concentration of $\displaystyle Y$ has no bearing on the rate of reaction.

We can therefore write $\displaystyle -\frac{d[Y]}{dt} = k$ where k is the rate constant from step 2. In the exercises the student is asked to show that the cocnetartion of Y decreases linearly .

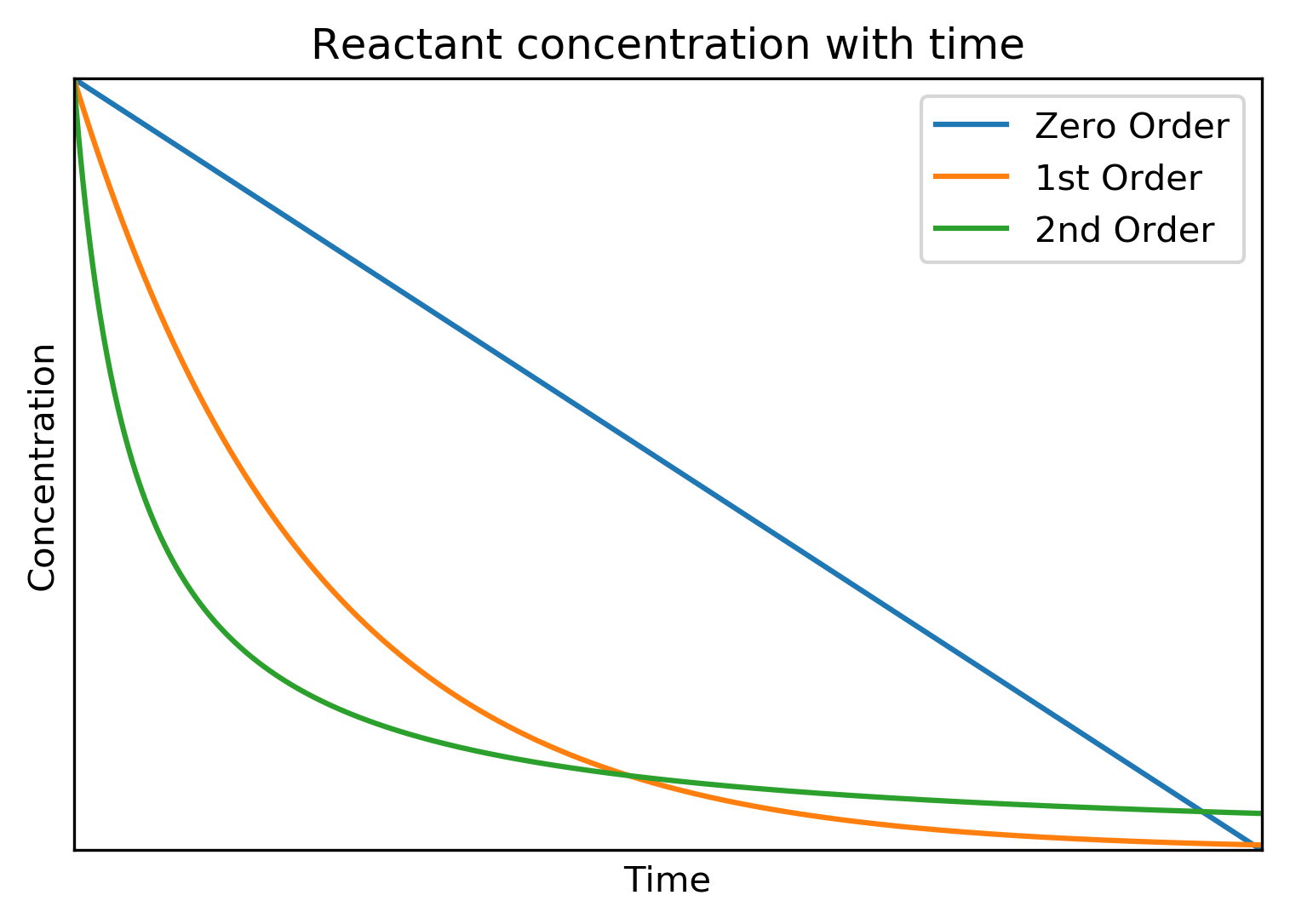
Below is shown concentration profiles for zero, 1st and 2nd order reactions.

alt text