Oxbridge-Science-Academy.github.io

Concentrations of Products

Back to Chemical Kinetics Home
Copyright Oxbridge Science Academy 2022

The previous section looked at how we can derive expressions for the variation of a reactant with time for first and second order reactions. However, we are often interested in the time-dependence of product formation a well. For example, many drugs are delivered to the body not in their active form but as a precursor which will react in the body, sometimes multiple times, to eventually form the molecule which is biologically active and performs the specific therapeutic task. It is relatively straightforward to express the concentration of product as a function of time in a reaction of simple stoichiometry. The key step is to remember that mass is conserved.

First Order Reactions

Consider again the reaction $\displaystyle X \rightarrow Y$ . The change in denoted $[X]$ (denoted $\Delta [X]$ ) will be equal to the (negative) change in denoted $\displaystyle \Delta [Y]$ . This can be expressed as:

$\displaystyle \Delta [X] = - \Delta [Y]$

The mass balance equation can as be expressed as:

$\displaystyle [X]_0 = [X] +\ [Y]$

Where $\displaystyle [X]_0$ is the initial reactant concentration.

The reaction $\displaystyle X \rightarrow Y$ is first order in $\displaystyle X$ and so the $\displaystyle [X]$ can be written as:

$\displaystyle [X] = [X]_0e^{-kt}$

Substituting this into the mass balance equation yields an equation for the product concentration $\displaystyle [Y]$ as a function of time:

$\displaystyle [X]_0=[X]_0e^{-kt} +\ Y$

$\displaystyle \Rightarrow Y = [X]_0 \left(1-e^{-kt} \right)$

Again it is worth considering if an equation makes sense under certain conditions (a so-called “sanity check”) - this is good practice in all areas of the science.

At the start of the reaction $\displaystyle t=0$ , there will be no product, i.e. $\displaystyle [Y]=0$ .

Substituting $\displaystyle t=0$ into the expression:

$\displaystyle Y = [X]_0 \left(1-e^{0} \right) = [X]_0(1-1) = 0$

As the reaction time tends $\displaystyle \rightarrow \infinity$ , there will be only product and no reactant. The product concentration will be equal to the initial reactant concentration, $\displaystyle [X]_0$ . Substituting $\displaystyle t=\infinity$ into the expression for $\displaystyle [Y]$ :

$\displaystyle [Y]=[X]_0\left(1-e^{-\infinity}\right) = [X]_0$

Thus, the equation of product concentration as a function of time meets these two conditions. It is important to note that performing such sanity checks does not mean the expression is definitely correct; rather is a quick way of spotting if is wrong.

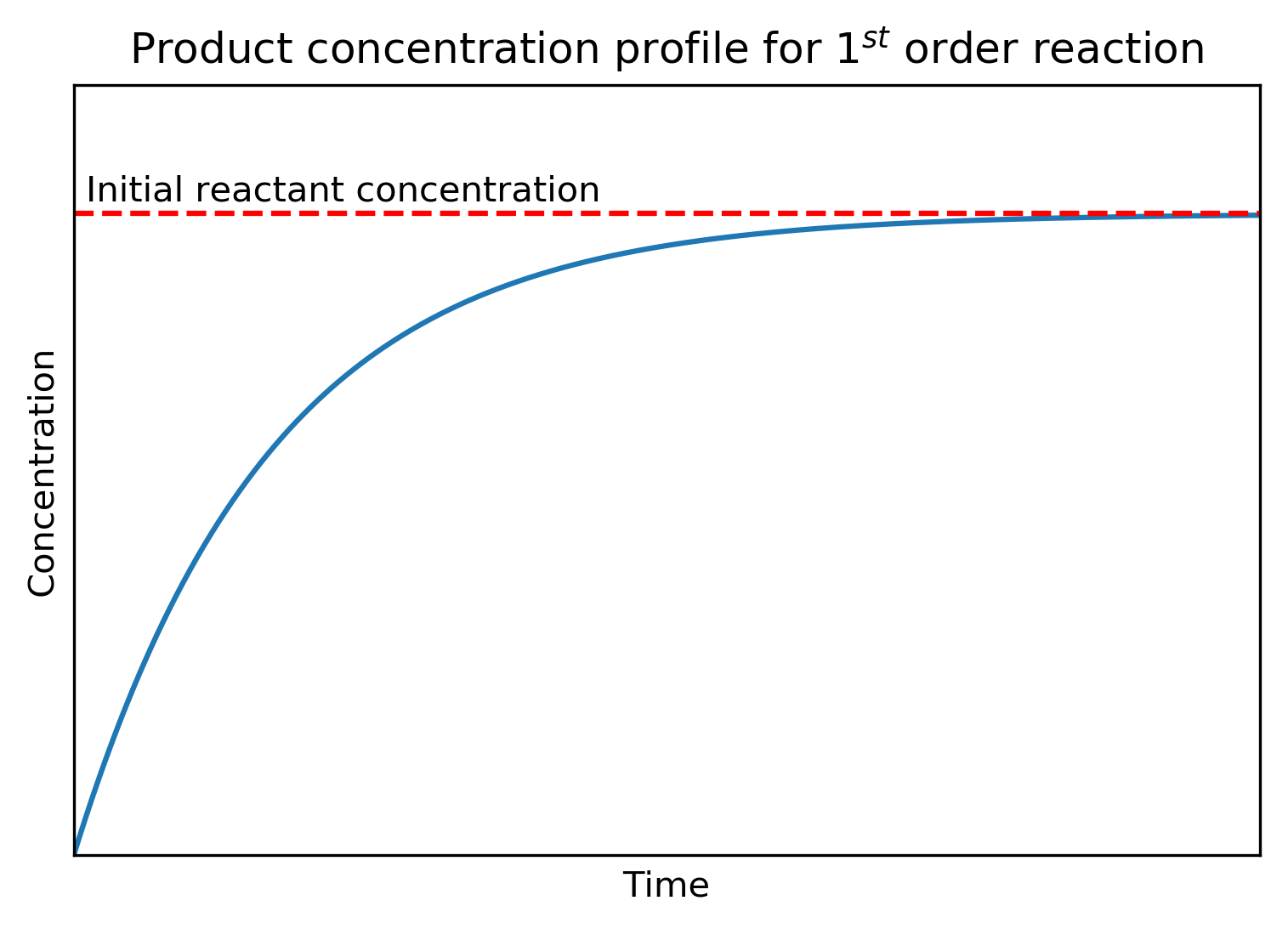
The expression for $\displaystyle [Y]$ is plotted below. We can see how the product concentration increases rapidly at first, coinciding with the region of most rapidly reactant loss, before plateauing and tending to the concentration of the initial reactant concentration. Incidentally, the same mathematics is observed during the charging of a capacitor and will be familiar to those of you who studied A Level (or equivalent) Physics.

drawing

Other Order Reactions

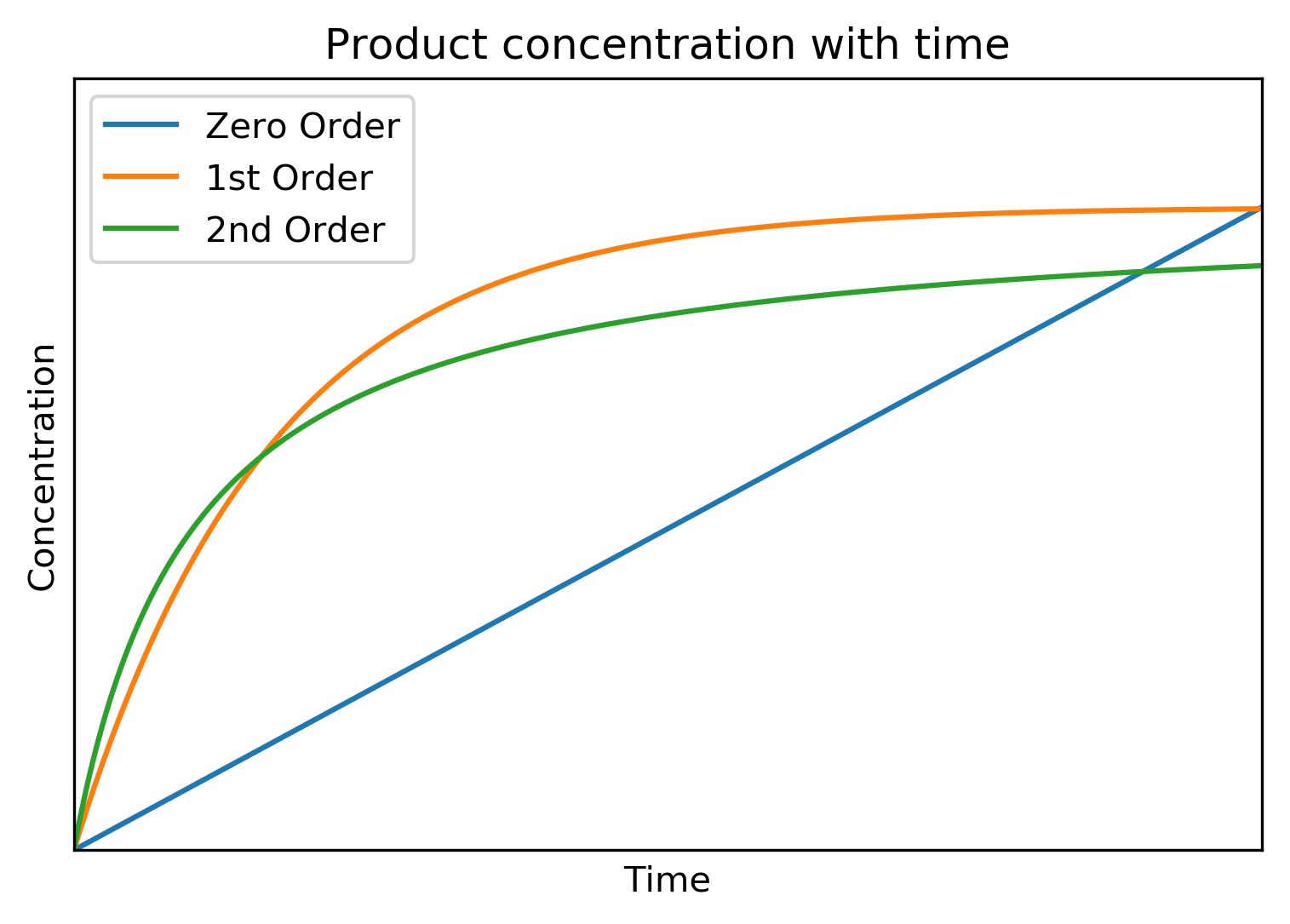
Below are the shown the product concentration profiles for zero, 1st and 2nd order reactions. Note that the product concentartions mirror the reactant concentartion profile shown earlier.

drawing