Oxbridge-Science-Academy.github.io

Rate Constants

Back to Chemical Kinetics Home
Copyright Oxbridge Science Academy 2022

You are likely to encountered rate constants (also referred to as rate coefficients) before. They allow the temperature dependence on rates of reaction to be expresesd matheamtically. While not always the case, the majority of the reactions you will encounter in undergraduate chemistry speed up with temperature - they have a positive temperature dependence.

The temperature dependence is represented in the rate constant, $\displaystyle k$ :

$\displaystyle k=Ae^{-\frac{E_a}{RT}}$

Where $\displaystyle A$ is the pre-exponential factor (temperature independent to a first approximation), $\displaystyle E_a$ is the activation energy, $\displaystyle R$ is the gas constant and $\displaystyle T$ is the temperature in Kelvin.

Determining rate constant parameters

A plot of $\displaystyle k$ against $\displaystyle T$ produces a curve from which it is hard to extract information about the parameter of interest, $\displaystyle E_a$ . This is shown below for the reaction of $O +\ O_3 \rightarrow O_2 +\ O_2$ :

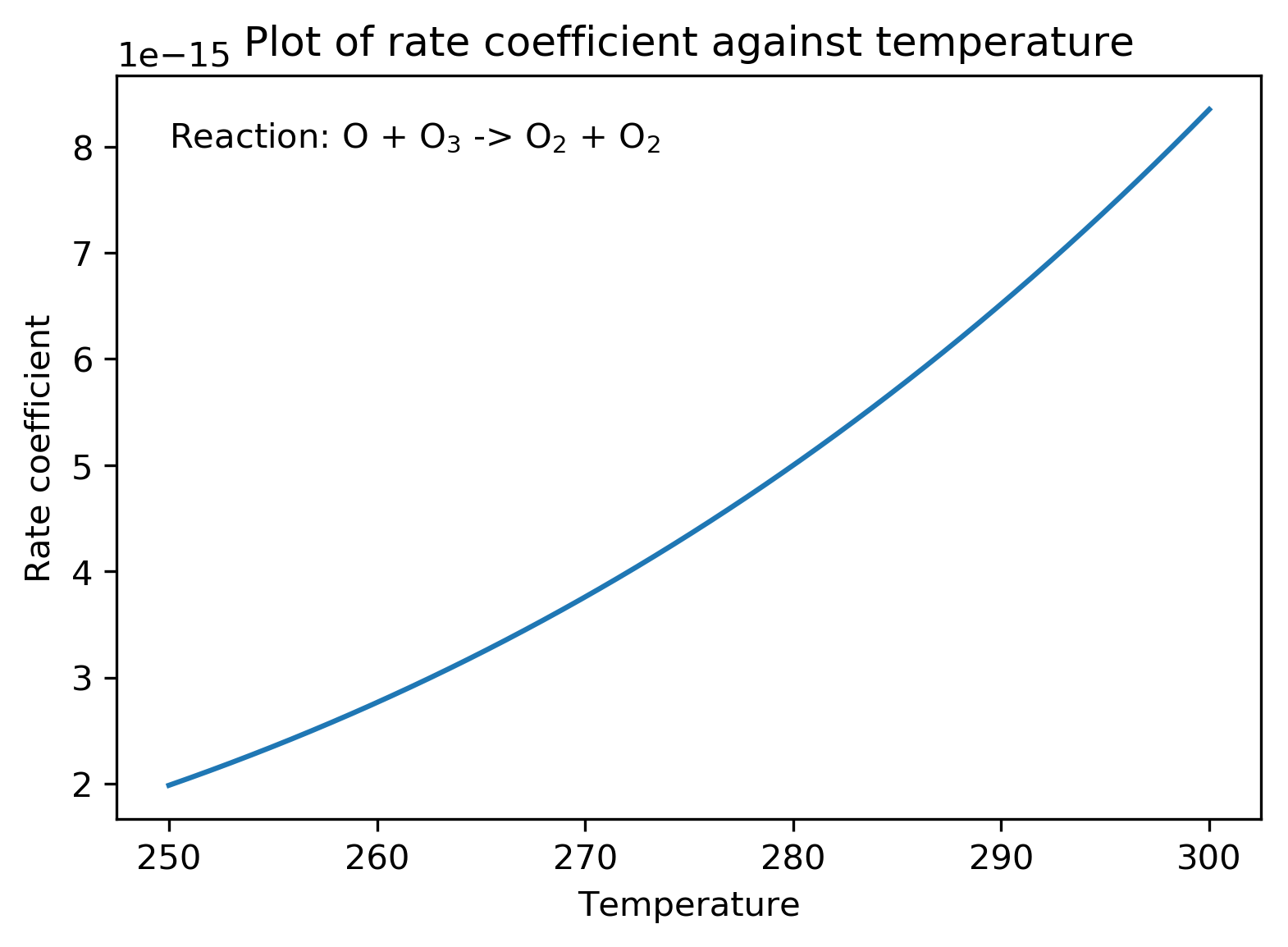
alt text

However, we can manipulate the expression for $\displaystyle k$ to produce a straight line plot from which it is easier to determine important parameters.

Taking the natural logarithm of both sides:

$\displaystyle \ln k = \ln Ae -\frac{E_a}{RT}$

Plotting $\displaystyle \ln k$ against $\frac{1}{T}$ will produce a straight line with gradient $-\frac{E_a}{R}$ as shown below.

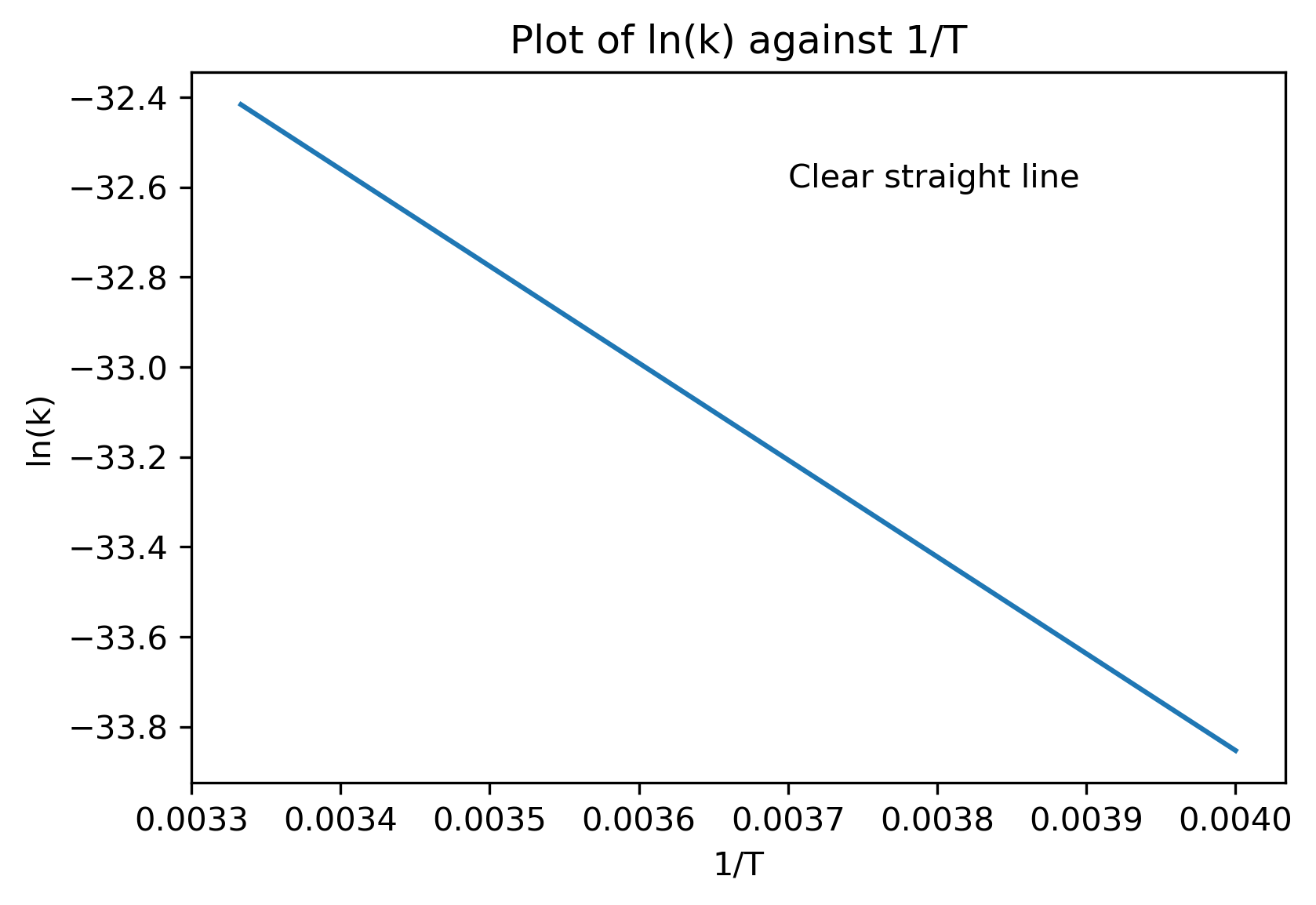
alt text

Pre-Exponential Factor

While the exponential part of the rate constant allows us to include a temperature dependence, it is clear what the role of the pre-exponential factor is. So far we have made no acknowledgement of the fact that molecules are not spherically symmetric particles. The particular symmetry of atomic and molecular orbitals mean that particles must collide with a particular orientation to allow sufficiently good orbital overlap for a new bond to form. This orientational factor is included in the pre-exponential factor, $\displaystyle A$ . This term does display a (weak) temperature dependence (~ $T^{\frac{1}{2}}$ ) but this is beyond the scope of this course and is usually negligible compared to the strong temperature dependence caused by the exponential term.

The $\frac{E_a}{RT}$ term is dimensionless as required and so is the exponential term as a whole. Therefore, the dimensions of the rate constant (see next section) are the same as the dimensions of the pre-exponential factor. It is important to remember that cannot compare a pre-exponential factor from first order and second order reactions directly just as we cannot compare rate constants for a first order and a second order reaction directly.

Dimensions of the Rate Constant

Unlike equilibrium coefficients which are strictly dimensionless, the units of a rate coefficient depend on the overall order of the reaction - the sum of the powers of the relevant species’ concentrations. The dimensions of reaction rate are concentration per unit time with the most common units used being mol dm^-3 s^-1 for aqueous phase reactions and molecules cm^-3 s^-1 for gas phase reactions. The dimensions of the rate coefficients must be such that the rate of reaction has the correct dimensions.

Consider a generic rate of reaction:

$\displaystyle rate = k[A]^{\alpha} [B]^{\beta} [C]^{\gamma} ...$

When considering the dimensions, we can merge all the concentration terms in a single concentration raised to a power, $\displaystyle n$ , which is the sum of all the individual powers: